论文阅读-Collecting and Analyzing Multidimensional Data with Local Differential Privacy

标题：Collecting and Analyzing Multidimensional Data with Local Differential Privacy
作者：Ning Wang, Xiaokui Xiao, Yin Yang, Jun Zhao, Siu Cheung Hui, Hyejin Shin, Junbum Shin, Ge Ye
发表会议：ICDE 2019

---

• 1 Introduction
• 2 Preliminaries
• 3 Collecting A Single Numeric Attribute
• 4 Collecting Multiple Attributes
• 5 Stochastic Gradient Descent under Local Differential Privacy
• 6 Experiments
• 7 Related Work
• 8 Conclusion

首先回顾一下之前提到的1BitMean机制（论文：《Collecting Telemetry Data Privately》）

Collection mechanism 1BitMean: When the collection of counter $x_i(t)$ at time $t$ is requested by the data collector, each user $i$ sends one bit $b_i(t)$, which is independently drawn from the distribution:

$$b_i(t) = \begin{cases} 1 & \text{with probability} \frac{1}{e^\epsilon+1}+\frac{x_i(t)}{m}\cdot\frac{e^\epsilon-1}{e^\epsilon+1} \\ 0 & \text{otherwise} \\ \end{cases}$$

在分析的时候，之前也说过这个公式的本质实际上就是一个映射机制，将 $[0,m]$ 的数据映射到概率空间 $[\frac{1}{e^\epsilon+1}, \frac{e^\epsilon}{e^\epsilon+1}]$ 中，再以这个概率决定反馈的数据是0还是1。有了这个了解，我们来看一下论文中提到的 Duchi’s Solution for One-Dimensional Numeric Data，其算法如下所示：

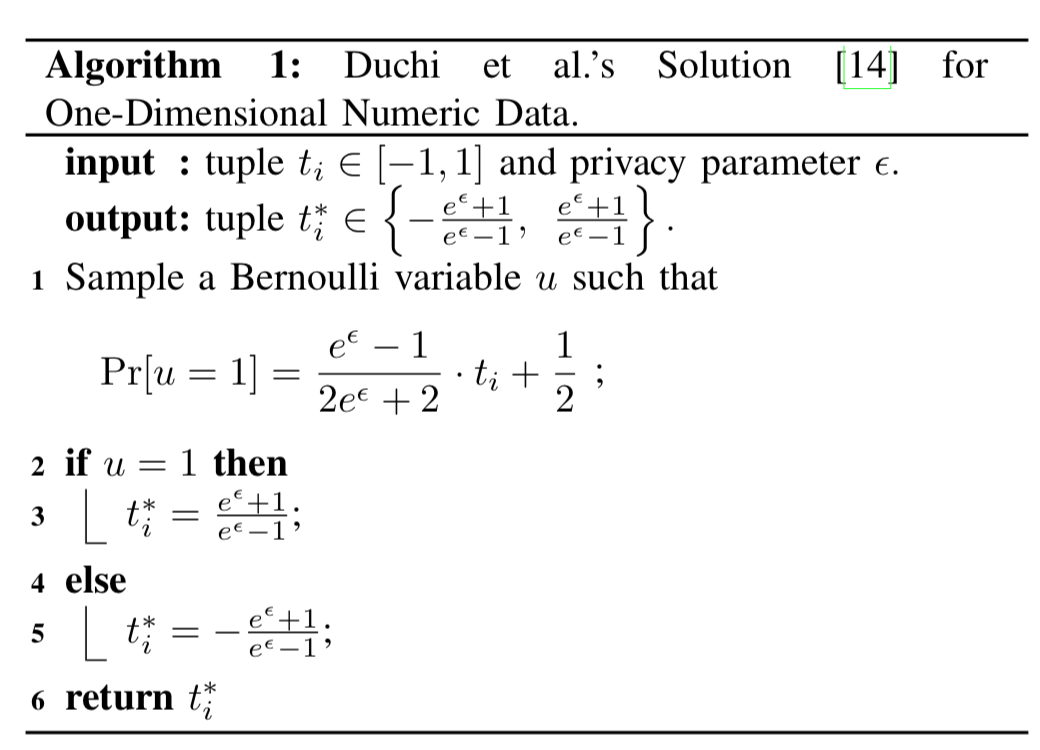
这个算法中，输入的原始数据范围是 $[-1, 1]$，映射方程的设计过程如下，假如 $y = k \cdot t_i+b$，将$(-1, \frac{1}{e^\epsilon+1}),(1, \frac{e^\epsilon}{e^\epsilon+1})$，两点带入，可得：

$$\begin{cases} \frac{1}{e^\epsilon+1} = -k + b \nonumber \\ \frac{e^\epsilon}{e^\epsilon+1} = k + b \nonumber \end{cases}$$

我们就可以解得：

$$\begin{cases} k = \frac{1}{2} \cdot \frac{e^\epsilon-1}{e^\epsilon+1}\nonumber \\ b = \frac{1}{2} \nonumber \end{cases}$$

这也就意味着，概率的映射函数为：

$$\Pr[u = 1] = \frac{e^\epsilon-1}{2e^\epsilon+2}\cdot t_i + \frac{1}{2}$$

根据上面的过程，我们就将数据映射到了$\{0,1\}$, 接下来我们就需要计算期望了：

$$\begin{align} E[u] &= 0 \times \Pr[u=0] + 1\times \Pr[u=1] \nonumber\\ &= \frac{e^\epsilon-1}{2e^\epsilon+2}\cdot E[t] + \frac{1}{2} \nonumber \end{align}$$

所以如果将数据映射到$\{0,1\}$，还需要在估计的均值上面再做一个线性的映射才能估计出原始数据的均值。那么，能不能再进一步免去这个过程呢。我们可以这样想，考虑到原始数据是对称的，那么我们能不能不将数据映射到$\{0,1\}$，而是映射到$\{-A, A\}$，使得我们不需要在估计的均值之后还需要进一步处理估计的数据，我们来看看，能不能做到。在这个假设下，均值可以这么计算：

$$\begin{align} E &= -A \times \Pr[u=0] + A \times \Pr[u=1] \nonumber\\ &= A \cdot (2\Pr[u=1]-1) \nonumber\\ &= A \cdot \frac{e^\epsilon-1}{e^\epsilon+1}\cdot E[t] \nonumber \end{align}$$

因此，如果令$A=\frac{e^\epsilon+1}{e^\epsilon-1}$，即可满足$E=E[t]$，这样子也就不需要估计了均值之后再进行一步映射了。

接下来我们以另一种角度理解一下为什么这样的算法（实际上是这一类算法）可以满足DP呢？下图中的$-1$和$1$代表$y=-1$和$y=1$。

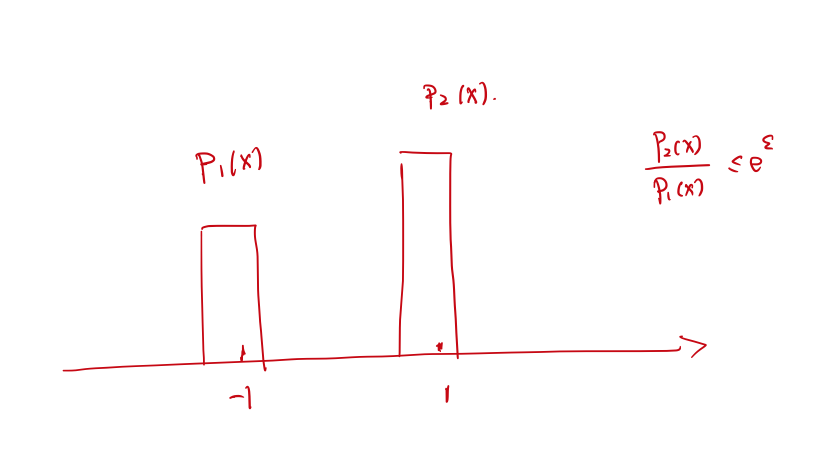
如果既想满足DP又想做均值估计，那么以下两点必须要达到（这是我总结的，欢迎来反驳）：

• 概率要求：$p_1(x)+p_2(x) = 1$
• DP要求：$p_2(x) / p_1(x) \le e^\epsilon$
• 均值估计要求：$\mathbb{E}[p_1(x)]$必须与$x$是线性的

在第三点均值估计的要求中，为了在匿名数据中直接得到原始数据的均值，也可以理解为$\mathbb{E}[p(x)] = x$，为了做到这点我们可以将数据范围进行放缩，比如Duchi’s Solution中，原始数据范围是$[-1, 1]$，匿名数据范围却是$\{\frac{e^\epsilon+1}{e^\epsilon-1},-\frac{e^\epsilon+1}{e^\epsilon-1}\}$，这个是很好做的，仅仅把数据进行一个放缩就好了，因为映射关系是线性的。

在我们以前的案例中，所接触到的映射的结果都是离散的，比如Duchi’s Solution中结果只有-1和1两种情况。所以我们就会想，能否对于一个$x$，我们映射到一个分布呢，即：这里的$p(x)$是一个分布，而不是一个离散的值。

即，假设我们要把$[-1, 1]$的数据映射到范围$[-C, C]$的话，大概是这样，如下图所示（在图上标注不方便，我下文中用高的和矮的表示概率密度函数中高的部分和矮的部分）：

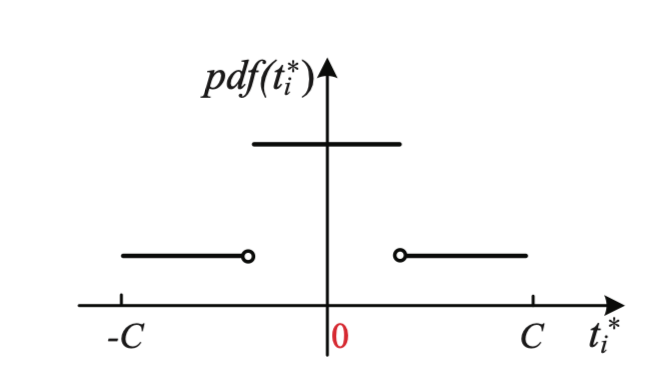
那么现在问题又来了，我们重新看一下上面提到的三个要求：

• 概率要求：概率和需要为1，即在概率密度函数中，面积要为1。
• DP要求：即高的对应的面积比低的对应的面积上界是$e^\epsilon$
• 均值估计要求：这个要求好像现在好像比较难处理

所以，这个高的部分的中心并不是当前的值$x$，比如当$x=1$的时候为了使得发布数据的期望为$x$，应该是这样的：

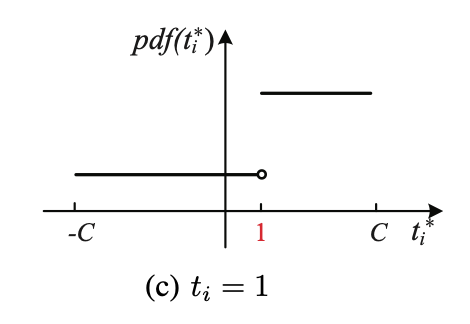
我们先来看概率要求，假设高的概率值为$p$（并不是说高的概率，因为概率是面积），那么矮的值就是$p / e^\epsilon$，所以概率要求在这里就是：

$$p \cdot (C-1) + p/e^\epsilon \cdot (C+1)= 1$$

接下来我们再看均值估计的要求，我们注意到，当$x=0$的时候，高的部分的中点其实就是0，当$x=1$的时候，我们来看看怎么计算均值：

$$E = p \cdot (C-1) \cdot \frac{1+C}{2} + \frac{p}{e^\epsilon}\cdot(C+1) \cdot \frac{1-C}{2}=1$$

根据以上过程可以求得 $C$ 和 $p$ 的值：

$$\begin{align} &C = \frac{\exp(\epsilon/2)+1}{\exp(\epsilon/2)-1} \\ &p = \frac{\exp(\epsilon) - \exp(\epsilon/2)}{2\exp(\epsilon/2)+2} \end{align}$$

因此，我们就可以得到基于这个概率分布的均值估计方法了，作者取名叫做Piecewise Mechanism。

$$pdf(t_i^*=x|t_i) = \begin{cases} p, \quad\quad \text{if} \quad x \in [l(t_i), r(t_i)]\\ \frac{p}{\exp(\epsilon)}, \quad \text{if} \quad x \in [-C, l(t_i)) \cup (r(t_i), C] \end{cases}$$

其中：

$$\begin{align} &C = \frac{\exp(\epsilon/2)+1}{\exp(\epsilon/2)-1} \\ &p = \frac{\exp(\epsilon) - \exp(\epsilon/2)}{2\exp(\epsilon/2)+2} \\ &l(t_i) = \frac{C+1}{2}\cdot t_i - \frac{C-1}{2} \\ &r(t_i) = l(t_i) + C-1 \end{align}$$

不过我觉得 $pdf$ 公式这么写容易让人摸不着头脑，当然可能是因为我没有相应的数学背景，我想这是一个条件概率，判断的$x$应该属于条件中，比如 $\Pr[y=a|x] = 1/x \quad\text{if}\quad x=1$，这种才是让人理解的吧，而不能写成 $\Pr[y=a|x] = 1/x \quad\text{if}\quad y=1$。

再多说一句，为什么我们在分析的时候没有提到$l(t_i),r(t_i)$呢，实际上这也是不一定需要的，这里的$l,r$，其实是为了计算那个高的从哪里开始从哪里结束。在我们的分析过程中，我们已经知道这个高的长度为$C-1$了，那么我们只需要知道中心点就好了。我们提到过如果要想均值估计，那么这个映射肯定是线性的，所以把$(0,0), (1, \frac{C+1}{2})$两点联立一个方程就知道中心店的变化是$center = \frac{C+1}{2}t_i$，然后$l=center-\frac{C-1}{2}$，就可以知道$l,r$是啥了。

这个公式出来了，肯定是要继续求一下均值和方差的，均值的求法论文里用的是积分，当然，对于这么简单的变换实际上不用积分也可以求，用这个就可以了：

$$\begin{align} \mathbb{E}(t_i^*) &= \frac{p}{e^\epsilon} \cdot (l(t^*)+C) \cdot (\frac{-C+l(t^*)}{2}) \nonumber\\ &+ p \cdot (r(t^*)-l(t^*))\cdot \frac{l(t^*)+r(t^*)}{2} \nonumber\\ &+ \frac{p}{e^\epsilon} \cdot (C-r(t^*)) \cdot \frac{C+r(t^*)}{2} \nonumber \end{align}$$

方差的话，只能按照论文中的公式去进行求解，利用

$$Var[t_i^*] = \mathbb{E}[(t_i^*)^2]-(\mathbb{E}[t_i^*])^2$$

---

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。